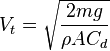daught
Well-known member
Campfire argument:
If you drop two balls that are shaped the same and they have the same coefficient of friction, but different weights does the heavier one reach a higher terminal velocity? This is in regular still air NOT vacuum.
If you drop two balls that are shaped the same and they have the same coefficient of friction, but different weights does the heavier one reach a higher terminal velocity? This is in regular still air NOT vacuum.